Generating random directions with uniform distribution
The Common approach
When writing particle system, one often needs to choose random direction vectors for particle velocities. It is desirable to have velocities with uniform distribution (ie. the same amount of particles is shot in every direction). The most common approach is to use rand() function to generate x, y and z components of velocity vector, which is then normalized:
const int n_vertex_num = 0x50000;
Vector3f p_vertex_list[n_vertex_num];
float f_rand()
{
return float(rand()) / RAND_MAX * 2 - 1;
// generates random number in range [-1, 1] with uniform distribution
}
void Init()
{
for(int i = 0; i < n_vertex_num; ++ i) {
Vector3f v_rand(f_rand(), f_rand(), f_rand());
v_rand.Normalize();
p_vertex_list[i] = v_rand;
}
}
This leads to:
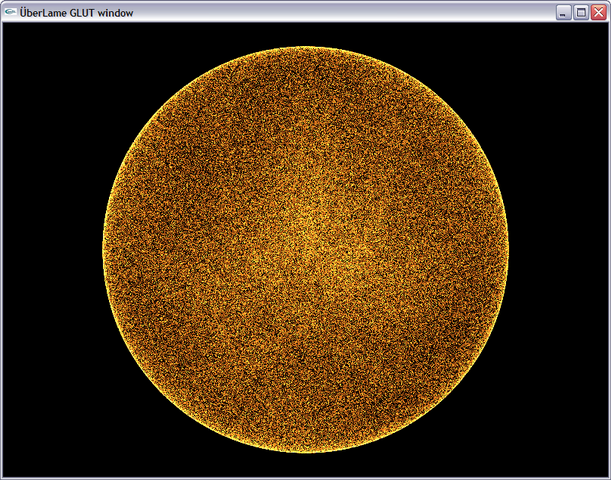
This is image of velocity vectors, displayed as points on unit sphere. It is apparent that in some directions there is far more particles than in average.
Making it uniform
When generating velocities using f_rand(), those are placed inside unit cube. Cube is then projected onto a sphere. It is obvious that some portions of cube project to smaller area than the other ones, therefore resulting in denser particles in that particular direction.
This can be fixed by simply changing distribution of numbers generated by f_rand(). This means it is going to generate more of small numbers and less of large numbers. Then the unit cube is no longer filled uniformly with velocity vectors and when doing non-linear projection of cube onto a sphere, non-uniform distribution is compensated and we get uniformly filled sphere. We can change f_rand() to this:
float f_rand2()
{
float f = f_rand();
return f / cos(f);
}
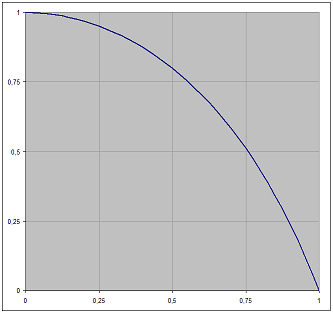
On the image above, there is histogram of f_rand2() results (absolute values). It says it generates a lot of values arround zero and less values with absolute value near to one. This actually fixes the problem as can be seen on the following image:
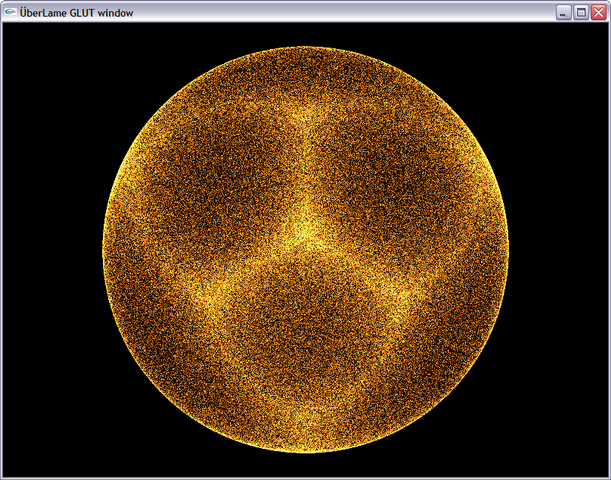
These images depict results generated by original f_rand() (left) and modified f_rand2() (right) without normalization:

What about GPU?
In case it's necessary to generate particle velocities on GPU, we run into a little trouble: on GPU, there's no rand() function. What to do about it? We can use perlin noise as pseudo-random number generator.
Assume particle velocities should be rendered to some texture (where rgb maps to xyz). We take texture coordinates as parameters to noise function. Ideal white noise (ie. random) function should show no correlation between noise samples. When sampling perlin noise with normalized OpenGL texture coordinates (values in range [0, 1]), correlation will be rather apparent because perlin noise is continuous. What we can do is to scale texture coordinates to increase noise frequency which fixes the problem. Scaling factor should be higher than noise period, not divisible by it and in the same time not too high so GPU's FPU can still work with it. Values between 1000 and 10000 worked well for me.
uniform float seed; // frame time can be used as seed
const vec4 magic = vec4(1111.1111, 3141.5926, 2718.2818, 0);
// some magic numbers (any real random numbers of sufficient magnitude will do)
void main()
{
vec2 tc = gl_TexCoord[0].xy * magic.xy;
// scale texture coordinates
vec3 skewed_seed = vec3(seed * magic.z + tc.y - tc.x) + magic.yzw;
// scale and skew seed a bit to decrease noise correlation accross pixels
// (add some magic numbers to generate three seeds to decrease correlation
// between velocity coordinates)
vec3 velocity;
velocity.x = noise(tc.x, tc.y, skewed_seed.x);
velocity.y = noise(tc.y, skewed_seed.y, tc.x);
velocity.z = noise(skewed_seed.z, tc.x, tc.y);
// use noise to generate random direction
// (permutate arguments to decrease correlation even more)
velocity = normalize(velocity);
// normalize
gl_FragColor.xyz = velocity * 0.5 + 0.5;
// pack to unsigned RGB
}
Note GLSL specification defines some noise functions, but they aren't implemented on current hardware so it's necessary to supply noise() function implementation. Stefan Gustafson's noise code proven to be most useful (use google).
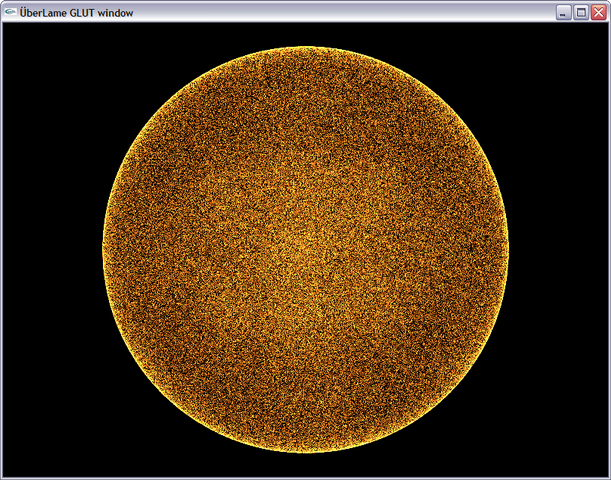
Code above is GLSL fragment shader which generates random directions parametrized by uniform variable seed. Note the directions are stored as unsigned RGB in the same fashion as normals in normalmap. The following image shows the results of the shader copied to vertex buffer object and rendered as points. Note there is no need to modify distribution of perlin noise because it is not linear by nature and particles are distributed uniformly: