Today we're going to have some real fun. We're going to talk about collision detection in 2D which offen includes some highly-interactive demos. I'd actually like to write a simpler space game and then a little bit more complicated arcade game.

We've actually implemented very simple and quite fast collision detection function for 2D already. It's polygon overlap test. But it gives a little less information about collision than we need (it actually returns boolean "true - collision occured" / "false - no collsison") So what is it we need from our collision detection routine anyway?

To say what we need from collision detection it's necessary to talk about how our simulation is going to work. Basically all physics simulation can be divided into two steps - collision detection and collision response.

Imagine we have some scenario with some particles (in 2D - circles) which are affected by gravity and bounce as they hit each other. Every particle has it's mass and velocity. Our simulation step will be a simple loop responsible for simulating some time span of particle movements. It will begin with detecting time of first collision, move all particles along their trajectories to that point in time, then apply impulse on colliding particles (affect their velocities in such a manner they're moving away from each other) and repeat again until we have particles in positions at the end of the given time span. In case no collision occured we can just move particles and return right away. To better explain the process, i wrote a few lines of pseudocode:

void SimulationStep(float f_time_span)
{
    ApplyGravityOnParticles(f_time_span);
    // accelerate particles towards earth

    do {
        CParticle &r_a, &r_b;
        float f_time_of_collision = f_GetFirstCollision(r_a, r_b);
        // find first collision and colliders

        if(f_time_of_collision > f_time_span) {
            TranslateParticles(f_time_span);
            return;
        }
        // in case no collision occured in this time span,
        // just move particles and we're done

        TranslateParticles(f_time_of_collision);
        // translate particles to the moment they collide

        f_time_span -= f_time_of_collision;
        // calculate remaining time

        Vector3f v_impulse = r_a.v_Pos() - r_b.v_Pos();
        v_impulse.Normalize();
        // begin with unit vector with direction objects need
        // to be pushed away from each other

        v_impulse *= v_impulse.f_Dot(r_a.v_Velocity() - r_b.v_Velocity());
        // scale impulse by projection of relative velocities
        // of objects to impulse axis

        v_impulse *= f_bounce_ratio;
        // scale impulse some more to get style of collisions we want
        // f_bounce_ratio = 1 would give perfectly plastic collisions
        // (objects would stick to each other)
        // f_bounce_ratio > 1 would make objects bounce away

        r_a.v_Velocity() -= v_impulse * .5f;
        r_b.v_Velocity() += v_impulse * .5f;
        // apply impulse to objects
    } while(f_time_span > f_epsilon);
    // repeat till we reach the end of the given timespan
}

It looks quite simple, doesn't it? And it is mostly simple but there's always our numeric imprecission lurikng in the darkness so it always needs some tuning and sometimes even different handling for moving objects and objects in peace.

Basically what it does is it lets move particles until two of them collide. Then it stops movement, calculates new velocities for those collifing particles ("pushes them away from each other") and continues moving particles again until another pair collides. On and on again.

Let me focus on impulse calculation for a while. Impulse is basically velocity colliding particles are going to be accelerated by. First we calculate contact point and collision axis. Contact point is point where colliding objects meet (that is necessary to give spin to colliding objects) and collision axis is common normal vector of colliding objects surfaces. For particles we can skip both as particles are in fact points and they don't exhibit rotation in any way (in our simulation) and collision axis always goes from center of first particle to the center of second one. As soon we have collision axis, we project relative velocity of particles on it (relative velocity is speed particles are approaching each other) Then we scale it by some constant and add it to current particle velocity so particles are no longer approaching and so collision is solved. Because of numerical stability, particles will sometimes penetrate each other so we may need to push them away a little (by "manually" offseting their positions, typically only by fraction of necessary distance; fraction only is used to prevent creating another penetrations to other nearby particles)

I was talking about particles all the time. In convex madness series we're dealing with some convex shapes so we're going to need function that would give us time to collision for two moving polygons as well as collision conact point and axis. It's quite a lot of job, but it's not so complex as it may sound.

Separating axis theorem is very popular method for determining wheter objects are colliding, how far they can move before collision occurs and of course as the name suggests we will get our axis of collision. (we're not going to simulate object rotations for now so we can skip contact point calculation ... we'll get to it a bit later) Moreover it's easily extendable to 3D space and it can be also used for collinion of polygonal objects with analytical objects such as spheres (cirlces in 2D), rays and all that stuff. However, i'm going to cover the polygon collision part only this time.

So ... how does it work? Separating axis theorem basically says that in case it's possible to draw an axis that would separate two objects from each other, objects do not collide. (in 3D space it will be separating plane) How do we pick such a separating axis? It's simply one of polygon edge axes. There's nothing complicated about that.

Now when we have lots of candidates for separating axis (all edges of both polygons tested for collision), how to determine wheter axis is separating? We simply create perpendicular axis and project polygon vertices on it. The result is two intervals where each polygon begins and where polygon ends, in 1-dimensional space of the axis. You can see such a separating axis on the following image. Right edge of quad was chosen as separating axis. Under it there's another axis perpendicular to it and on that axis we can see two intervals (red and green) depicting projections of both polygons to the axis:

Wee can see those polygons do not collide and so says the separating axis: intervals of polygon projections are disjunct (they do not overlap) In case we couldn't find any such axis it means the polygons are in collision:

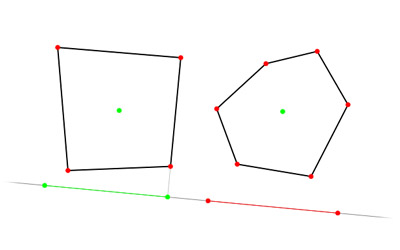
It can be clearly seen the intervals are conjunct (they do overlap). It's also noticeable that in case we'd shift one of polygons along the axis intervals lie on by distance intervals overlap the polygons would not collide anymore. So that axis can be sure used as collision axis.

Now that we see everything would work for us the question may arrise by what criterion i chose those lucky axes. They're simply axes with the smallest overlap (in case no separation axes exist) or axes with the greatest distance between intervals. You can see all separating axes for those two polygons on the following image:

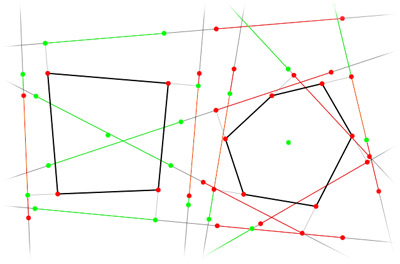
It's really a mess, but if you look at it thoroughly, you can see the separating axis i chose in the first image is really an axis with the greatest distance between projection intervals.

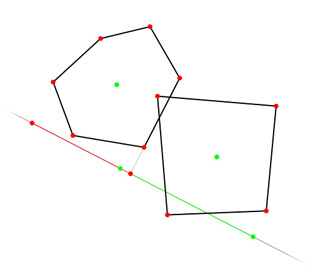
Now get back to our collision detection. We can find separating axis and tell how far apart the objects are. But it assumes the objects don't move. In case both objects are in motion, we need to make a simple modification to the algorithm. First it's necessary to calculate relative velocity of objects which is simply difference of velocities of both objects. Then, when calculating intervals, velocity vector is projected to the axis as well and is added to one of intervals (with respect to difference sign) and we get a new interval distances (or overlaps) which needs to be compared with respect to relative speed of polygons projected to axis in question. Such a calculation would require a couple of divisions so we can do it another way.

Instead of using velocity vectors we use displacement vectors. (displacement is velocity times time span length) We add displacements to intervals as well but now we can compare interval distances (or overlaps) without any rescaling. To demonstrate this i've prepared another image:

I hope you liked this one, another could follow soon enough. If you see any typos or factual errors, let me know ... Any feedback is pleasant, in general.